Algoritma : Queue

Rumahit.ID - Queue disebut juga antrian dimana data masuk di satu sisi dan keluar di sisi yang lain. Karena itu, queue bersifat FIFO (First In First Out). Antrian (Queue) merupakan suatu  kumpulan data yang penambahan elemennya (masuk antrian) hanya bisa dilakukan pada suatu ujung (disebut dengan sisi belakang/rear) atau disebut juga enqueue yaitu apabila seseorang masuk ke dalam sebuah antrian. Jika seseorang keluar dari antrian/penghapusan (pengambilan elemen) dilakukan lewat ujung yang lain (disebut dengan sisi depan/front) atau disebut juga dequeue yaitu apabila seseorang keluar dari antrian.

Jadi, dalam antrian menggunakan prinsip “masuk pertama keluar pertama” atau disebut juga dengan prinsip FIFO (first in first out). Dengan kata lain, urutan keluar akan sama dengan urutan masuknya. Contoh : antrian mobil saat membeli karcis di pintu jalan tol, antrian di bioskop dan sebagainya.

Operasi / Prosedur Standar pada QUEUE (ANTRIAN)

QUEUE merupakan struktur data dinamis, ketika program dijalankan, jumlah elemennya dapat berubah secara dinamis sesuai keperluan. Berikut ini operasi-operasi standar pada queue :

• Inisialisasi, merupakan prosedur untuk membuat queue pada kondisi awal, yaitu queue yang masih kosong (belum mempunyai elemen).
• InQueue, Insert Queue merupakan prosedur untuk memasukkan sebuah elemen baru pada queue. Jumlah elemen Queue akan bertambah satu dan elemen tersebut merupakan elemen belakang.
• DeQueue, Delete Queue merupakan prosedur untuk menghapus/mengambil sebuah elemen dari queue. Elemen yang diambil adalah elemen depan dan jumlah elemen queue akan berkurang satu.

Hal lain yang perlu diperhatikan dalam suatu struktur dinamis adalah jumlah elemen struktur data tersebut. Operasi-operasi yang berhubungan dengan jumlah elemen suatu queue adalah :

1. Size, yaitu operasi untuk mendapatkan banyaknya elemen queue.
2. Empty, yaitu prosedur untuk mengetahui apakah queue dalam keadaan kosong atau tidak. Dengan status ini maka dapat dicegah dilakukannya operasi Dequeue dari suatu queue yang kosong.
3. Full, merupakan prosedur untuk mengetahui apakah Queue penuh atau tidak. Prosedur ini hanya berlaku untuk queue yang jumlahnya terbatas.

IMPLEMENTASI ANTRIAN DENGAN ARRAY

Karena antrian merupakan suatu kumpulan data, maka tipe data yang sesuai untuk menyajikan antrian adalah menggunakan array atau list (senarai berantai).

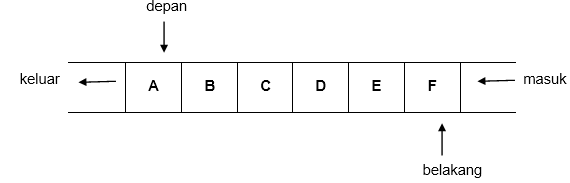
Perhatikan gambar berikut ini :

Contoh Antrian Dengan 6 Elemen

Gambar di atas menunjukkan contoh penyajian antrian menggunakan array. Antrian di atas berisi 6 elemen, yaitu A, B, C, D, E dan F. Elemen A terletak di bagian depan antrian dan elemen F terletak di bagian belakang antrian. Jika ada elemen baru yang akan masuk, maka elemen tersebut akan diletakkan di sebelah kanan F. Dan jika ada elemen yang akan dihapus, maka A akan dihapus terlebih dahulu.

Elemen A terletak di bagian depan, kemudian disusul elemen B dan elemen yang paling belakang.

Gambar 2 menunjukkan antrian di atas dengan penambahan elemen G dan H, sehingga gambar 1. Menjadi :

Contoh Penambahan Antrian Dengan 2 Elemen

Contoh Penghapusan Antrian Dengan 2 Elemen

Seperti pada tumpukan atau stack di dalam antrian juga dikenal 2 operasi dasar yaitu menambah elemen baru yang akan diletakkan di bagian belakang antrian dan menghapus elemen yang terletak di bagian depan antrian. Selain itu kita juga harus melihat antrian itu mempunyai isi atau masih kosong.

Untuk memahami penggunaan antrian dalam array, kita membutuhkan deklarasi antrian, misalnya sebagai berikut :

# define MAXN 6
Typedef enum { NOT_OK, OK } Tboolean; Typedef struct {
Titem array [MAXN]; int first;
int last;
int number_of_items;
} Tqueue

Dengan deklarasi di atas, elemen antrian dinyatakan dalam tipe integer yang semuanya terdapat dalam struktur. Variabel first menunjukkan posisi elemen pertama dalam array, dan variabel last menunjukkan posisi elemen terakhir dalam array.

Algoritma dari penggalan program di atas adalah :

1. Tentukan elemen yang akan dimasukkan ke dalam antrian (dalam hal ini adalah 6 elemen).
2. Deklarasikan struktur untuk menampung elemen pada antrian.
3. Selesai.

Untuk menambah elemen baru dan mengambil elemen dari antrian dalam antrian, diperlukan deklarasi berikut ini :

void initialize_queue ( Tqueue *Pqueue)
{
     Pqueue -> firs = 0; 
     Pqueue -> last = -1;
     Pqueue -> number_of_items = 0;
}

Tboolean enqueue ( Tqueue *Pqueue, Titem item)
{
    if (Pqueue -> number_of_items >= MAXN) 
        return (NOT_OK);
    else {
        Pqueue -> last++;
        if (Pqueue -> last > MAXN -1) 
        Pqueue -> = 0;
        Pqueue -> array[Pqueue->last] = item; 
        Pqueue ->  number_of_items++; 
        return (OK);
    }
}

Tboolean dequeue (Tqueue *Pqueue, Titem, item)
{
     if (Pqueue -> number_of_items == 0) 
         return (NOT_OK);
     else {
         *Pitem = Pqueue -> array[Pqueue->first++]; 
         if (Pqueue -> first > MAXN -1)
         Pqueue -> first = 0;
         Pqueue -> number_of_items--; 
         return (OK);
     }
}

Penggalan program di atas apabila dikelompokkan berdasarkan fungsinya adalah sebagai berikut :

1. Deklarasikan Antrian
void initialize_queue ( Tqueue *Pqueue)
{
   Pqueue -> firs = 0; 
   Pqueue -> last = -1;
   Pqueue -> number_of_items = 0;
}

2. Fungsi untuk memasukkan elemen pada antrian adalah sebagai berikut :
Tboolean enqueue ( Tqueue *Pqueue, Titem item)
{
    if (Pqueue -> number_of_items >= MAXN) 
        return (NOT_OK);
    else {
        Pqueue -> last++;
        if (Pqueue -> last > MAXN -1) 
        Pqueue -> = 0;
        Pqueue -> array[Pqueue->last] = item; 
        Pqueue ->  number_of_items++; 
        return (OK);
     }
}

3. Fungsi untuk menghapus elemen pada antrian adalah sebagai berikut :
Tboolean dequeue (Tqueue *Pqueue, Titem, item)
{
    if (Pqueue -> number_of_items == 0) 
        return (NOT_OK);
    else {
       *Pitem = Pqueue -> array[Pqueue->first++]; 
       if (Pqueue -> first > MAXN -1)
       Pqueue -> first = 0;
       Pqueue -> number_of_items--; 
       return (OK);
    }
}

Untuk memperjelas masing-masing fungsi pada deklarasi di atas, perhatikan gambar 4 di
bawah ini :

Contoh deklarasi antrian dengan 6 ukuran

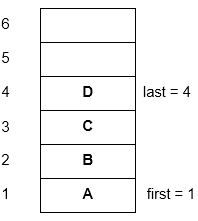
Dari gambar 4 di atas last dibuat = 0 dan first dibuat = 1 serta antrian dikatakan kosong jika last

< first.

Contoh deklarasi antrian penambahan 4 buah elemen

Dari gambar 5 di atas menunjukkan array dengan 6 elemen untuk menyajikan sebuah antrian (dalam hal ini MAXN  = 6). Pada saat permulaan antrian dalam keadaan kosong (gambar 4.) pada gambar 5 terdapat 4 buah elemen yang ditambahkan. Dalam hal ini first = 1 dan last = 4. Gambar 6 menunjukkan antrian setelah 2 elemen yaitu setelah A dan B dihapus.

Gambar 7 menunjukkan antrian baru setelah E dan F ditambahkan. Banyaknya elemen dalam antrian adalah 6-3+1=4 elemen

Contoh deklarasi antrian penghapusan 2 buah elemen

Contoh deklarasi antrian penambahan 2 buah elemen

Karena array terdiri dari 6 elemen, maka sebenarnya kita masih bisa menambah elemen lagi. Tetapi jika ingin ditambah elemen baru, maka nilai last harus ditambah 1 menjadi 7. Padahal array antrian hanya terdiri dari 6 elemen, sehingga tidak mungkin ditambah lagi, meskipun sebenarnya array tersebut masih kosong di dua tempat.

IMPLEMENTASI ANTRIAN DENGAN POINTER

Pada ilustrasi contoh di atas penambahan yang selalu dilakukan disebelah belakang antrian dan penghapusan yang selalu dilakukan pada elemen pada posisi paling depan, maka antrian sebenarnya juga merupakan bentuk khusus dari suatu senarai berantai (linked list). Jumlah elemen yang bisa diisi dalam antrian terbatas pada ukuran array yang digunakan.

Untuk memanipulasi sebuah antrian bisa digunakan dua buah variabel yang menyimpan posisi elemen paling depan dan elemen paling belakang. Apabila antrian diimplementasikan menggunakan linked list maka cukup 2 pointer yang bisa dipakai yaitu elemen paling depan (kepala) dan elemen paling belakang (ekor).

Untuk mengimplementasikan antrian dengan menggunakan pointer, perhatikan algoritma berikut ini :

1. Tentukan struktur untuk menampung node yang akan dimasukkan pada antrian. Deklarasi struktur pada penggalan program berikut ini :

struct queueNode
{
   char data;
   struct queueNode *nextPtr;
};
typedef struct queueNode QUEUENODE;
ypedef QUEUENODE * QUEUENODEPTR;
QUEUENODEPTR headPtr = NULL, tailPtr = NULL;

2. Deklarasikan penambahan elemen baru pada antrian, dimana letaknya adalah paling belakang. Deklarasi penambahan elemen baru tersebut dapat dilihat pada penggalan program berikut ini :

void enqueue ( QUEUENODEPTR *headPtr, QUEUENODEPTR *tailPtr, char value )
{
QUEUENODEPTR newPtr = malloc ( sizeof ( QUEUENODE ) );
     If ( newPtr != NULL )
     {
         newPtr -> data = value;
         newPtr -> nextPtr = NULL;
         if ( isEmpty ( *headPtr ) )
         *headPtr = newPtr;
     else
         ( *tailPtr ) -> nextPtr = newPtr;
     *tailPtr = newPtr;
}

3. Lakukan pengecekan terhadap antrian, apakah antrian dalam kondisi kosong atau tidak. Kalau kondisi antrian kosong, maka elemen bisa dihapus. Penggalan program berikut ini akan menunjukkan kondisi tersebut

int isEmpty ( QUEUENODEPTR headPtr )
{
    return headPtr == NULL;
}

Daftar Pustaka : 

Andri Kristanto, Algoritma & Pemrograman dengan C++ Edisi 2, Graha Ilmu, Yogyakarta, 2009.

Moh. Sjukani, Struktur Data [ Algoritma & Struktur Data 2 ] dengan C, C++, Mitra Wacana Media, Jakarta, 2008.

Teddy Marcus Zakaria dan Agus Prijono, Konsep dan Implementasi Struktur Data, Informatika, Bandung, 2006.