Algoritma : Struktur Pohon (Tree)

Definisi Pohon

Struktur pohon merupakan struktur data non linear. Pohon adalah susunan dari satu atau lebih simpul (node) yang terdiri dari satu simpul khusus yang disebut akar (root) sedang sisanya membentuk subtree dari akar.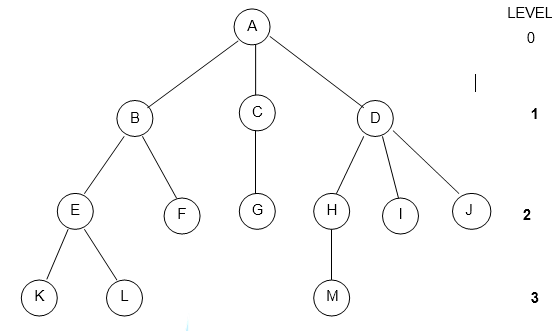

Akar dari struktur pohon ini adalah A
Satu simpul akan berisi :
* Informasi ( misal, A , B, dst)
* Cabang-cabang (Link) yang menghubungkan Kesimpul simpul yang lain.
Simpul A sebagai akar mempunyai 3 Link yang membentuk SUBTREE B,C, D. Jumlah SUBTREE dari satu simpul disebut : DERAJAT (DEGREE).

Derajat Simpul : A = 3 B = 2
C  =  1
G  =  0

Simpul yang mempunyai derajat = 0 disebut : SIMPUL TERMINAL atau DAUN (LEAF)
Contoh simpul daun gambar diatas adalah : K , L, F, G, M, I , J
Struktur Pohon yang terkenal adalah struktur geneologi (silsilah). Dalam struktur tersebut adanya simpul anak (children) dan orangtua(parent)
Contoh anak D adalah H, I, J
Orangtua D adalah A
Anak dari orang tua yang sama (saudara sekandung) disebut sibling misal H,I,J.

DERAJAT (DEGREE) SUATU POHON

Adalah derajat maksimum dari suatu simpul dalam pohon. Contoh derajat pohon dalam gambar diatas adalah 3.

Nenek Moyang dari dari suatu simpul adalah seluruh simpul-simpul yang ada sepanjang lintasan dari akar sampai simpul tersebut.

Contoh nenek moyang dari M adalah A, D dan H.

KEDALAMAN (HEIGHT atau DEPTH)

Kedalaman suatu pohon ditentukan oleh level maksimum dari simpul dalam pohon. Contoh kedalaman pohon dari gambar diatas adalah A.

HUTAN (FOREST)

Adalah susunan dari beberapa pohon.

Bila akar A dihilangkan maka akan diperoleh hutan dengan 3 pohon yaitu :

B(E(K,L),F) C(G) D(H(M),I,J)

Ada 2 cara untuk menyatakan struktur pohon yaitu :

1. Gambar

2. Daftar(List)

Pernyataan dengan Gambar adalah seperti terlihat pada Gambar diatas sedangkan kalau dengan List adalah sebagai berikut :

(A(B(E(K,L),F),C(G),D(H(M),I,J)))

Proses dalam struktur data non linier, bentuk pohon akan lebih mudah digambarkan bila diketahui :

1. n ( Jumlah Simpul atau Node )

2. k ( Derajat Pohon)

Dari data n dan k maka dapat dihitung :

JUMLAH LINK = n . k

JUMLAH NULL-LINK = n( k - 1)+1

JUMLAH NON ZERO LINK

STRUKTUR NODE K-ary = n - 1

Pohon 3 - ary :

Dari gambar diatas diket : n = 10 , k = 3
Maka dapat dihitung :

JUMLAH LINK                              = n . k   = 3. 10 = 30

JUMLAH NULL LINK                  = n ( k – 1 ) + 1

                                                        = 10( 3 – 1 ) + 1

                                                        = 21

JUMLAH NON ZERO LINK = n – 1 = 10 – 1 = 9

POHON BINER (BINARY TREE)

• Tipe yang sangat penting dari struktur data

• Dalam struktur pohon biner hanya dikenal SUBTREE KIRI DAN SUBTREE KANAN saja

Simpul dalam pohon biner adalah :

Susunan dari simpul-simpul yang masing-masing bisa kosong atau terdiri dari akar dan dua pohon biner yang terpisah dan disebut subtree kiri dan subtree kanan.

Pohon Biner Penuh ( Full Binary Tree)

Adalah pohon biner yang mempunyai simpul atau node lengkap dari level 1 sampai level ke I

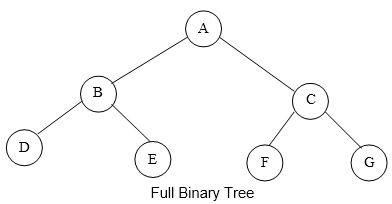
Pohon Biner Lengkap ( Complete Binary Tree)

Adalah pohon biner yang mempunyai simpul dengan nomor urut 1 sampai dengan n. 

LEVEL	ANAK TERKIRI	ANAK TERKANAN
1	1	1
2	2	3
3	4	7
4	8	15
5	16	31
6	32	63
7	64	127
8	128	255
9	256	511
10	512	1023
.	.	.
.	.	.

No anak kiri (Left Child) = No. Parent * 2

No anak kanan (Right Child) = (No. Parent *2) + 1

Pertanyaan

1.  Pohon dengan simpul jumlah simpul = 273 merupakan lengkap atau penuh
2. Berapa kedalamannya ?
3. No berapa simpul terkiri dari level tersebut ?
4. berapa jumlah maxsimum simpul level 7
5. No berapa anak kanan dari simpul ke 180 ?…..ada dilevel berapa anak tersebut.
6. No. berapa orang tua dari simpul ke 83 ? … ada dilevel berapa orangtua tsb

Kedalaman minimal dari pohon biner adalah :